本周主要讲解了一些优化的算法。
Mini-batch 梯度下降法
我们在执行梯度下降法时,会使用向量化的方法来加速计算。但如果训练集的数量很大时,速度仍然很慢。Mini-batch 梯度下降法可以加快训练的速度。使用传统的梯度下降法训练一次会处理所有的样本,而 Mini-btach 梯度下降法每次只处理部分的样本。
Mini-batch 梯度下降法每次处理样本的数量需要我们自己选择,设定的数量过大或过小都不合适。在极端情况下,设定数量为 1 (即随机梯度下降法,每次只处理一个样本),这样将失去向量化带来的加速效果,这样效率过于低下。设定数量为样本的总数时(即batch梯度下降法),单次迭代的速度会过慢。所以应将数量设置在中间的位置。
指数加权平均
后面将讲到一些高级的优化算法,在这之前需要了解“指数加权平均”的概念。
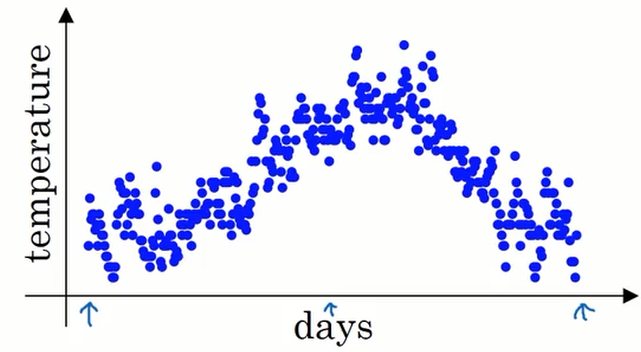
上图中蓝色的点表示伦敦在一年中每天的温度。
如果我们要计算趋势的话,也就是温度的局部平均值,我们可以这样做:
$\theta_i$ 表示第 i 天的温度。
$$
\large
v_0 = 0 \\
v_1 = 0.9v_0 + 0.1\theta_1 \\
v_1 = 0.9v_1 + 0.1\theta_2 \\
v_1 = 0.9v_2 + 0.1\theta_3 \\
v_1 = 0.9v_3 + 0.1\theta_4 \\
v_1 = 0.9v_4 + 0.1\theta_5 \\
…
$$
公式就是:$v_t = \beta v_{t-1} + (1-\beta)\theta_t$
下图中红色的线时 $\beta=0.9$ 的图像,绿色的线是$\beta=0.98$的图像。 $\beta$ 的值越大,曲线就越平缓,因为此时平均的天数更多,但也因为这样曲线进一步右移。可以看出绿色的线对于蓝色的点的趋势有一定的延迟。
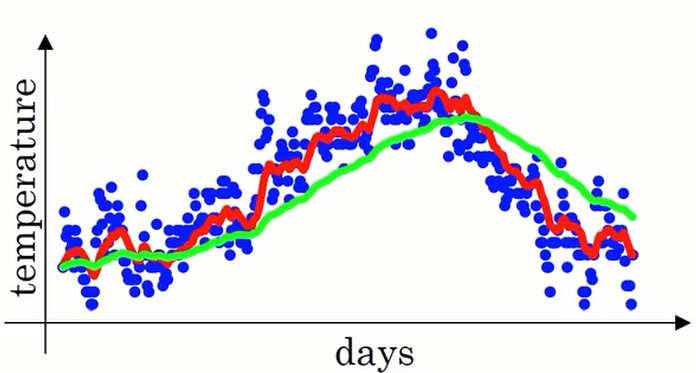
事实上,上面的图并不是实际的情况。如果我们设定$\beta = 0.98$ 我们得到的并不是绿色的线,而是下图中紫色的线。两条线相比,紫色线的起点更低,这是因为我们设置了 $v_0=0$,显然这与实际的数据是由出入的,即有偏差。
如果想修正偏差,可以将公式中的$v_t$换成$\frac{v_t}{1-\beta_t}$。其中 t 表示天数。当 t 很小时(且 $\beta < 0$),$v_t$ 除以一个小于 1 的数字将变大,当 $v_t$ 变得很大时,$\beta^t$ 约等于 0 ,$v_t$ 的值基本不变。
这样就实现了修正偏差。
然而在机器学习中人们并不在意修正偏差,而更愿意熬过初期获得更精确的预测值。如果你想在初期获得较精确的预测值,可以使用修正偏差。
动量梯度下降法
momentum 梯度下降法运行速度几乎总是快于标准的梯度下降法,其基本思想计算梯度的指数加权平均数,并利用该梯度更新权重。

上面是一个梯度下降的例子,因为样本中存在噪声,所以每一次梯度下降的方向并不是严格的指向最优点。这样在上下的方向上存在一个速度分量,我们看作是纵轴,左右方向上存在一个速度分量,我们看作是横轴。我们希望加快在横轴上的速度,而减缓在纵轴上的速度,这样可以更快的完成训练。
我们修改一下参数更新的公式,将上一节讲到的指数加权平均加入其中:
$$
\large
V_{dw} = \beta V_{dw} + (1-\beta)dw \\
V_{db} = \beta V_{db} + (1-\beta)db \\
w = w -\alpha V_{dw} \\
b = b -\alpha V_{db}
$$

上图中红色的线代表动量梯度下降法的轨迹,可以看到它在纵轴上的震荡变缓了。但是动量梯度下降法并不是在所有情况下都有效,它只对于碗状的函数有效。
RMSprop
RMSprop(root mean square prop)算法亦可以加速梯度下降,让我们来看看它是如何运行的。

同样的,我们希望可以加快在横轴上的学习,而减缓在纵轴上的学习。为了方便起见,将横轴上的参数记为 w ,纵轴上的参数记为 b ,我们将公式更新如下:
$$
\large
S_{dw} = \beta S_{dw} + (1-\beta)(dw)^2 \\
S_{db} = \beta S_{db} + (1-\beta)(db)^2 \\
w = w - \alpha \frac{dw}{\sqrt{S_{dw}}} \\
b = b - \alpha \frac{db}{\sqrt{S_{db}}}
$$
由图可知,在纵轴上的斜率较大,横轴上的斜率较小,即 $S_{db} > S_{dw}$ 。从公式中可以看到 dw 除以了一个较小的值,那么 w 的变化将变快。 db 除以一个较大的值 ,则 b 的变化将变小。
这就是 RMSprop 算法的思想。
需要注意的是,这里的 w 和 b 在实际的应用中可能是高维的向量。
为了防止发生除 0 的错误,我们做如下改动($\epsilon$ 是极小的值):
$$
\large
w = w - \alpha \frac{dw}{\sqrt{S_{dw}}+\epsilon} \\
b = b - \alpha \frac{db}{\sqrt{S_{db}}+\epsilon}
$$
Adam 优化算法
Adam(Adaptive Moment Estimation) 算法可以看作是 动量梯度下降算法 和 RMSprop算法 的结合。
这里直接给出公式,这里我们使用了修正偏差:
$$
\large
V_{dw} = \beta_1 V_{dw} + (1-\beta_1)dw ,
V_{db} = \beta_1 V_{db} + (1-\beta_1)db
\quad \leftarrow'momentun' \quad \beta_1
\\\
S_{dw} = \beta_2 S_{dw} + (1-\beta_2)(dw)^2 ,
S_{db} = \beta_2 S_{db} + (1-\beta_2)(db)^2
\quad \leftarrow 'RMSprop'\quad \beta_2
\\\
V_{dw}^{corrected} = V_{dw}/(1-\beta_1^t) ,
V_{db}^{corrected} = V_{db}/(1-\beta_1^t)
\\\
S_{dw}^{corrected} = S_{dw}/(1-\beta_2^t) ,
S_{db}^{corrected} = S_{db}/(1-\beta_2^t)
\\\
w = w - \alpha \frac{V_{dw}^{corrected} }{\sqrt{S_{dw}^{corrected}}+\epsilon} \\\
b = b - \alpha \frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\epsilon}
$$
这样就将两个算法结合起来了。
学习率衰减
加快学习算法的另一个方法就是随时间慢慢减少学习率,我们将它称为学习率衰减。
在训练的过程中,第一次遍历数据集我们记作 epoch 1,第二次记作 epoch 2 。。。 以此类推。
我们将学习率设为:
$$
\alpha = \frac{1}{1 + decay-rate * epoch-num}\alpha_0
$$
这样学习率就会随着迭代次数的增加而递减。
除此之外,还有多种方法进行学习率衰减,此处不一一列举。
局部最优的问题
过去研究人员会担心某些算法会陷入局部最优点,无法到达全局最优点。然而随着研究的深入,人们并不把这当作一个问题。
对于低维的数据在我们的脑海中往往出现这样一幅图像:
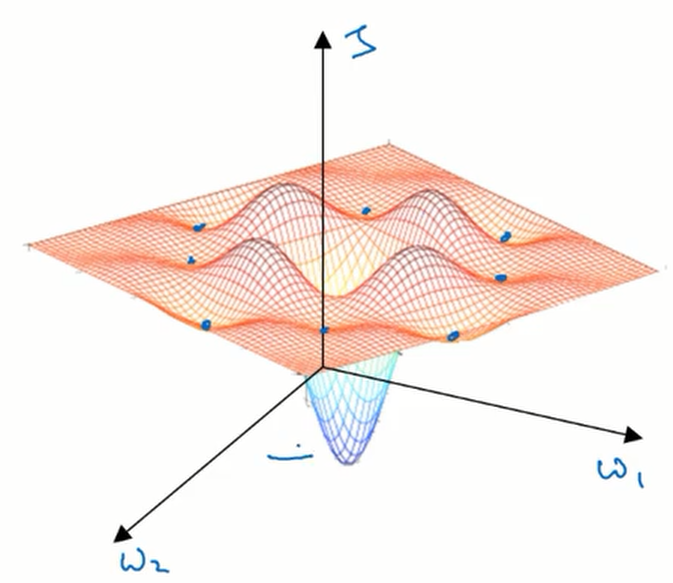
可以看到,在这幅图像中存在着许多局部最优点,可能会对算法造成影响。这样的想法影响了我们对高维数据的理解。在高维数据中我们通常不会遇到局部最优点,而是鞍点。
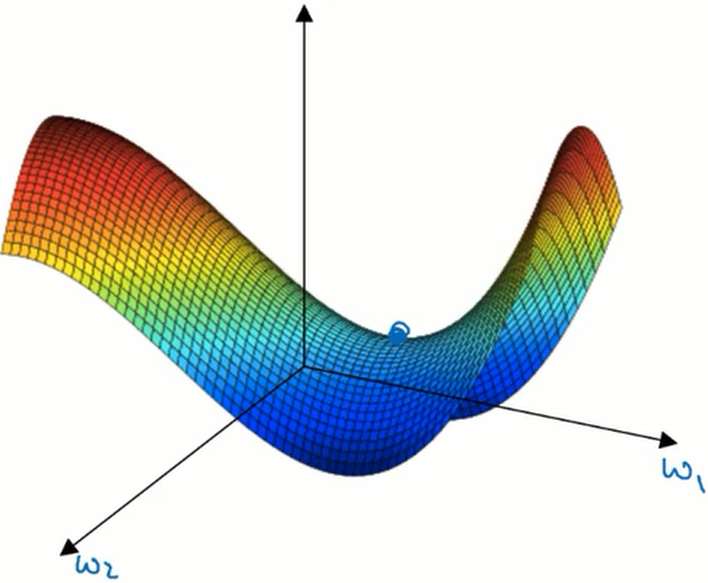
可以看到鞍点并不是在所有维度上的梯度都为 0 ,所以算法可以逃离鞍点。事实上,在高维的局部最优点很难遇到,它需要在各个维度上的梯度都为 0 才能满足,而这样点出现的概率非常低。所以说这并不是一个问题。
然而在算法达到鞍点时,训练的速度将变的十分缓慢,如何加速训练的速度这才是我们需要关注的问题。


