本周介绍了超参数调整,bath归一化以及程序框架的相关内容。
超参数调试
神经网络的改变会涉及到许多超参数的设置,这一节我们将介绍一些超参数调整的指导性原则。
虽然超参数的数量很多,但它们的重要性却不相同。例如超参数学习率 $\alpha$ 的重要性通常要高于其他的超参数。
在涉及多个超参数的调整时,我们可以根据下面的方法来处理:
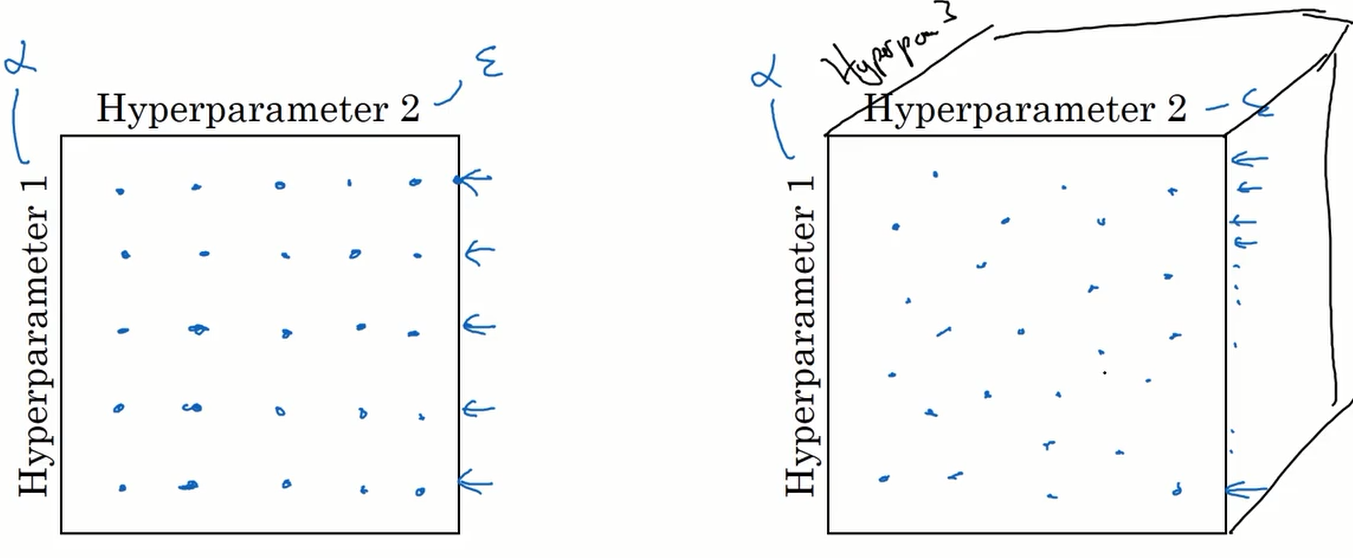
我们假设有两个超参数$\alpha$和$\epsilon$,如上图的左边,我们在网格中均匀的选取采样点进行测试。但因为超参数的重要性不同,$\epsilon$ 值的改变可能对结果没有影响,而$\alpha$的在这里只使用了 5 个值进行测试。
如果我们采用上图右边的方式,随机选取值来进行测试,这样就可使超参数的取值个数变多。
如果有三个超参数,那值的选取将在三维的立方体中进行。
另一个调整超参数的方法是”粗糙到精细” ,如果我们再网格中发现某一区域内的值较好,我们可以将此区域放大,进行更精细的取值。
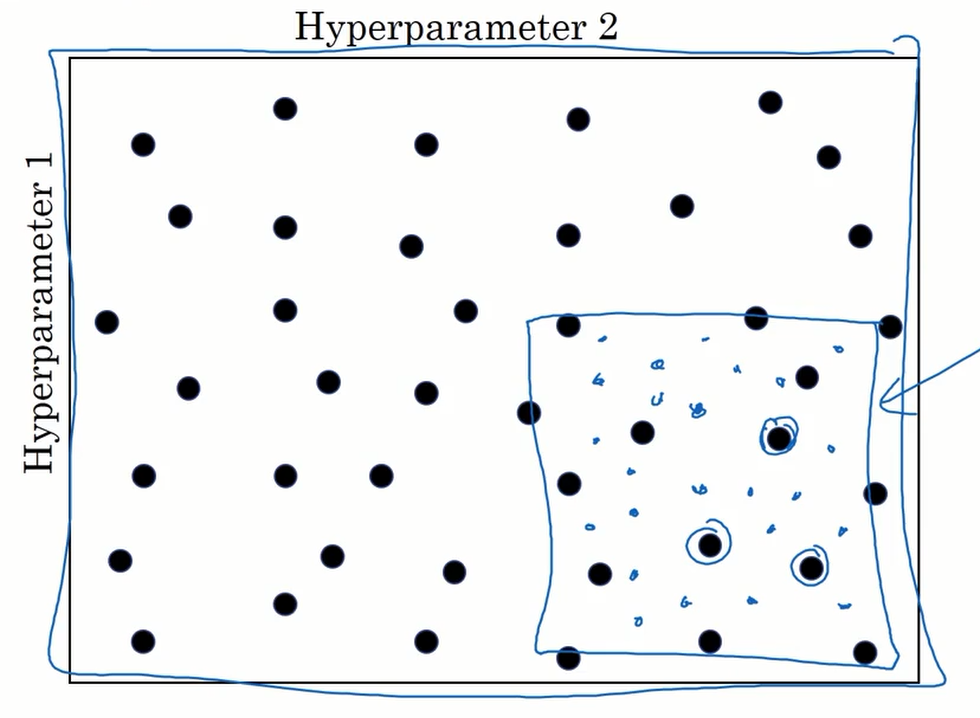
超参数范围选取
上一节中说到,随机取值可以提升你的搜索效率,但随机取值并不是在有效值范围内的随机均匀取值,而是选择合适的标尺用于探究这些超参数。
这里简单的说明随机均匀取值会有什么样的影响。假设参数 $\alpha$ 的取值范围是 0.0001 到 1 ,如果我们随机均匀取值的话,0.1 到 1 将需要 90% 的搜索资源,而 0.0001 到 0.1 只分到了 10% 的搜索资源,显然这并不是一个好的方法。
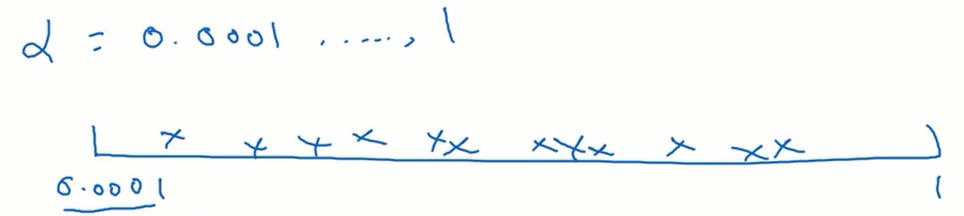
所以我们采用对数坐标轴来解决这个问题。我们在对数坐标轴上随机均匀取点,这样在 0.0001 到 0.001 之间就会有更多的搜索资源可用。
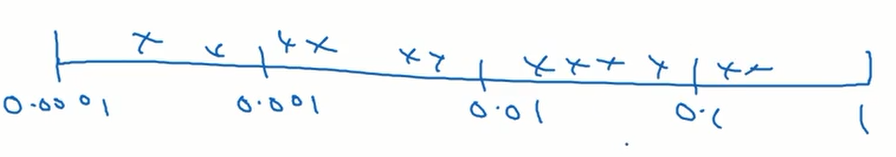
如果我们想将 $\alpha$ 的范围设置在 [0.0001,1] 之间,在 python 中 我们可以这样设置范围:
$$
\large
r = -4*np.random.rand() \leftarrow r \in [-4,0] \\
\alpha = 10^r \leftarrow \alpha \in [0.0001,1]
$$
Pandas VS Caviar
这里再给出一些设置超参数的方法。
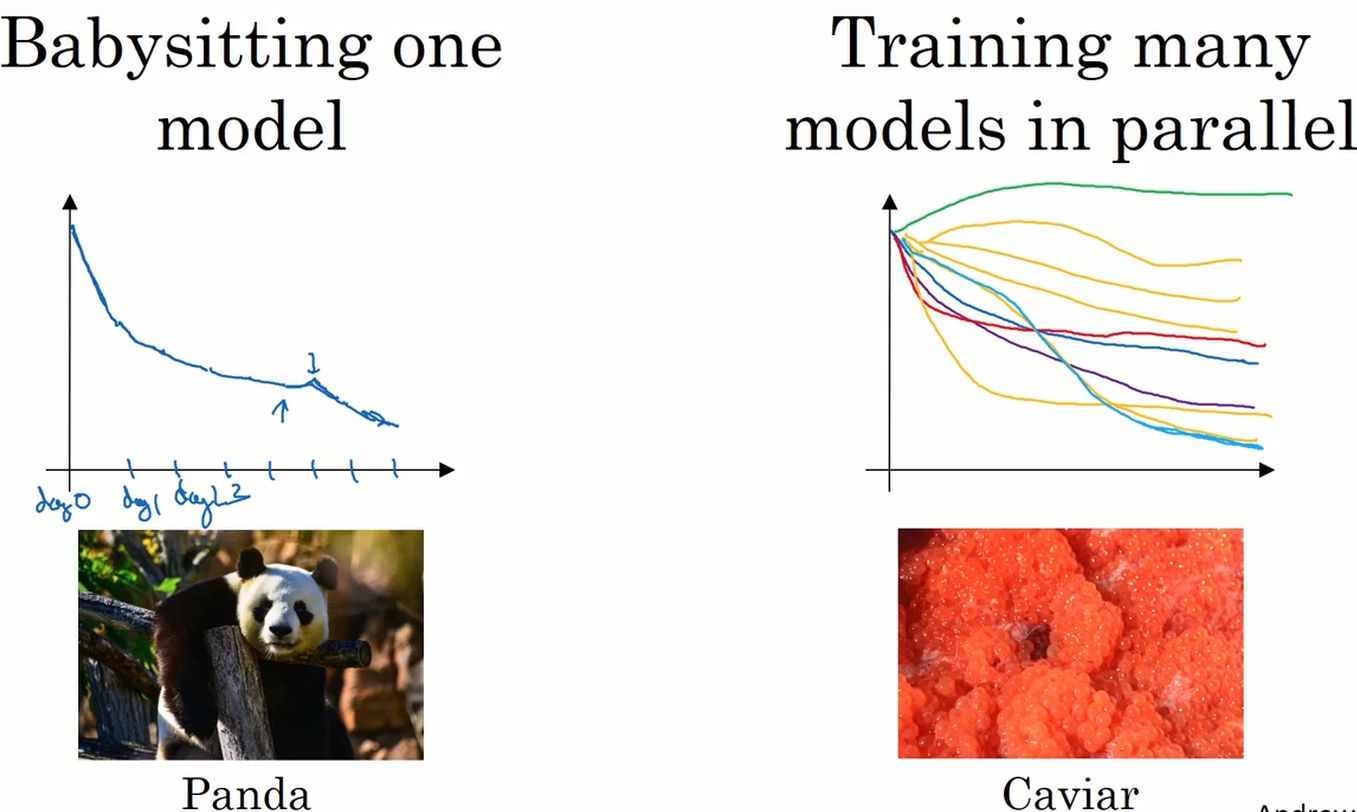
- 当我们的机器只能负担起实验一个模型或一小批模型时,我们通常采用这个方法。即每次实验一个模型,根据实验的结果修改超参数。然后再使用修改后的超参数训练模型,再根据此次实验的结果改进超参数,如此迭代。这种方法 AndrewNg 比喻为 pandas。
- 如果机器可以负担起多次平行实验,那就可以同时训练有不同超参数的模型,再根据实验的结果取得超参数的最优值。这种方法与鱼类生殖的方式相似,故比喻为 caviar(鱼子酱)。
batch 归一化
在前面的课程中我们提到过,归一化输入特征可以加速学习过程。
归一化的步骤如下:
$$
\large
\mu = \frac{1}{m}\sum x^{(i)} \\
x = x - \mu \\
\sigma^2 = \frac{1}{m} \sum (x^{(i)})^2 \\
x = x/ \sigma^2
$$
在神经网络中隐藏层的神经单元是没有输入特征的,所以我们要做的是对上一层传递过来的激活值进行归一化处理。
我们知道一个神经元计算过程可分为两步,第一步是加权求和得到 z 值,第二步是将 z 放入激活函数中求出激活值。 归一化的对象就是 z 。
下面是具体的步骤:
$$
\large
\mu = \frac{1}{m} \sum z^{(i)} \\
\sigma^2 = \frac{1}{m} \sum (z_i - \mu)^2 \\
z_{norm}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \epsilon}} \\
\widetilde{z}^{(i)} = \gamma z_{norm}^{(i)} + \beta
$$
这里 $\gamma$ 和 $\beta$ 的作用是可以随意设置 $\widetilde{z}$ 的平均值。如果不加入这两个参数,仅使用 $z_{norm}^{(i)}$ 作为最后的值,那么的平均值和方差是固定的。但我们并不想所有的隐藏单元都有同样的分布,这样才能学到有趣的特征,所以需要加入这两个参数。
需要注意的是,这两个参数也是需要学习的
下图展示了如何在深层神经网络中实现 batch 归一化。
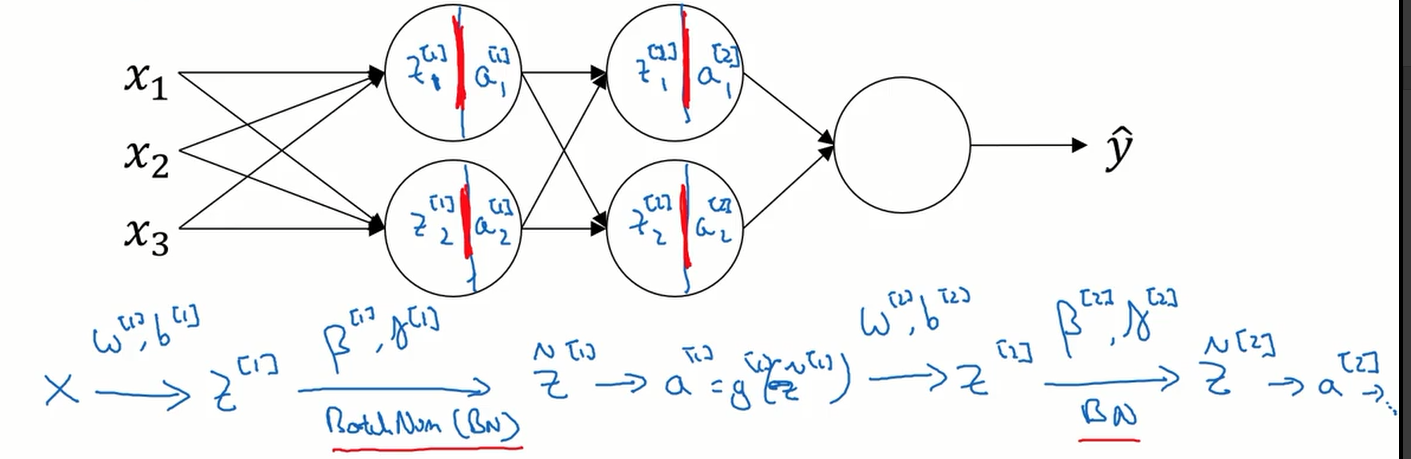
那么 batch 归一化 为什么有用呢? 可以这样理解,它减弱了前层参数的作用与后层参数的作用之间的联系,它使得每层网络可以自己学习,稍稍独立于其他层,这有助于加速整个网络的学习。
事实上,batch 归一化 还有一点轻微的正则化作用。
batch 归一化 常和 mini-batch 的方法一起使用。考虑这样一个问题,在测试时如何计算$\mu$ 和 $\sigma^2$的值呢?可以这样解决,在训练时可以记录下不同 mini-batch 下对应的 $\mu$ 和 $\sigma^2$。在测试时,使用指数加权平均的方法来估计两个参数的值。
softmax 回归
原理
到目前为止,所提到的分类例子都用了二分类,如果有多种分类的话可以使用 softmax 回归。我们来看看 softmax 的原理是什么:
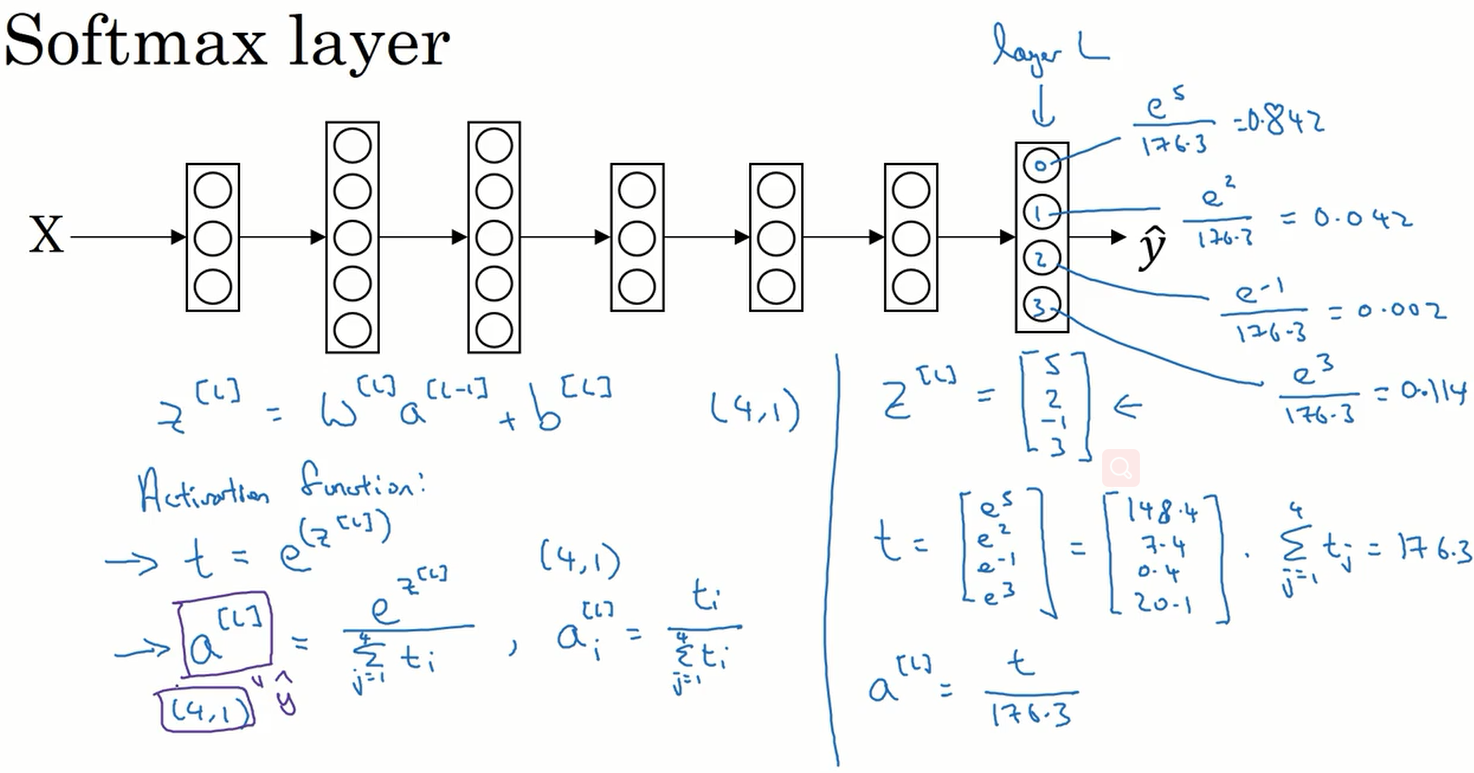
在神经网络的最后一层,先计算出 $z^{[l]}$ 的值,在将其输入到激活函数中。这里的激活函数输入值是一个向量,输出值也是一个同样维度的向量。思想就是将向量中的每个元素取幂,这样每个元素都为正数。再将每个元素除以所有元素之和,这样之后,所有元素均小于 1,大于 0 ,且所有元素之和为 0。最后向量的值可以看作是对应的概率。
$$
\large
z^{[l]} = w^{[l]}a^{[l-1]} + b^{[l]} \\
activation\quad function: \\
t = e^{(z^{[l]})} \\
a^{[l]} = \frac{e^{z^{[l]}}}{\sum^4_{j=1} t_i} \quad ,\quad a^{[i]}_i = \frac{t_i}{\sum^4_{j=1} t_i} \\
$$
代价函数
$$
\large
l(\hat{y},y) = -\sum^4_{j=1}y_j log\hat{y}_j
$$
其中 y 代表真实值, $\hat{y}$ 代表预测值。
$$
y^{(i)} = \begin{bmatrix}
0 \\ 1 \\ 0 \\ 0
\end{bmatrix} ,
\hat{y}^{(i)} = \begin{bmatrix}
0.3 \\ 0.2 \\ 0.1 \\ 0.4
\end{bmatrix}
$$
我们将对应的 y 值带入到代价函数中发现,如果对应真值的概率越高则代价越小,若概率越低则代价越大。


