在这个练习中,我们将实现逻辑回归算法,并将它应用到两个不同的数据集中。
逻辑回归
在这部分的练习中,你将创建一个逻辑回归的模型去预测某个学生能否进入大学。
假定你是大学招生办的主任,你想要通过两次测验的结果来决定申请人是否能获得入学资格。
你已经有了前面的申请人的历史数据,你可以将它作为逻辑回归的训练集数据。每一个训练样本中包括申请人两次测验的分数和是否获得了入学资格。
你的任务是建立一个分类模型使用申请人在两次测验的分数给出其能否入学的可能性。
可视化数据
如果可以的话,在实现任何学习算法之前先对数据进行可视化。
我们需要实现 plotData 函数来载入数据并将其可视化。
最后的结果应该如下图所示,两个坐标轴是两次测验的分数,并且正例和反例应该用不同的标记符号。
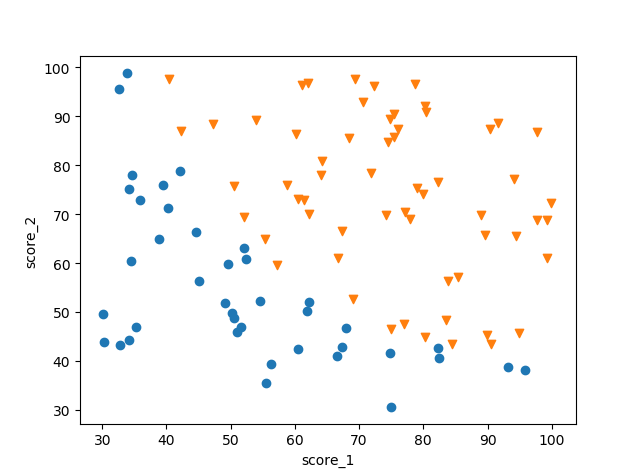
实现代码
1 | def loadData(file_path): |
实现
sigmoid函数
当你在开始实现代价函数之前,回忆一下逻辑回归的假设函数:
$$
\large h_\theta(x)=g(\theta^TX)
$$
其中 g 函数 就是 sigmoid 函数,sigmoid 函数的定义:
$$
\large g(z) = \frac{1}{1+e^{-z}}
$$
你的第一步是实现 sigmoid 函数,当你完成编码之后,最好测试一下你实现的 sigmoid 函数。当你使用很大的整数来测试时,返回的值应该趋向于 1 ,使用很大的负数时,返回的值应该趋向于 0 。使用 0 来测试时,得到的值应该是 0.5 。你实现的函数应该也可以适用于向量和矩阵。对于矩阵类型的参数,你的函数应该对矩阵中的每一个值进行计算。
1 | # simgoid 函数 |
代价函数和梯度
现在你将实现代价函数和梯度的计算。
逻辑回归中的代价函数:
代价的梯度是一个与参数 $\theta$ 有着同样长度的向量,第 j 个元素的定义如下:
$$
\large
\frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m}\sum_{i=1}^{m}{({h_\Theta}({x}^{(i)})-{y}^{(i)})}x_j^{(i)}
$$
需要注意的是,梯度的公式看起来与线性回归的公式是相同的,但因为假设函数的不同其实质是不同的。
当你实现 costFunction 函数之后使用初值为0的参数$\theta$计算初始的代价值,得到的结果应该是 0.693
1 | # 代价函数 |
学习参数
原作业中使用 octave 的 fminunc 函数来优化参数 $\theta$ , 这里我们使用 python scipy 库中的 optimize 函数来优化。
在这个函数中会调用你写好的 costFunction 函数来优化参数,optimize 函数给出的最后结果应该是:cost 约等于 0.203。
最后得到的 $\theta$ 值将会用来绘制决策边界,如下图所示: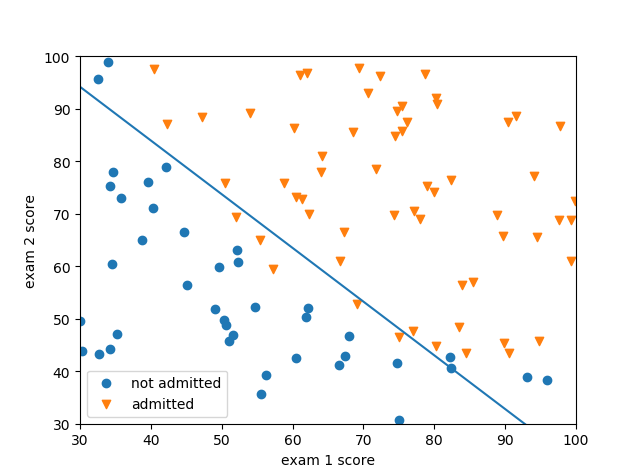
1 | import scipy.optimize as op |
评估逻辑回归
在学习参数之后,你可以使用这个模型去预测一个学生能否获得入学资格。
如果一个学生测试1的分数为45,而测试而的分数为85,那么他获得入学资格的可能性应该为 0.776。
另一个评估我们得到的参数的方式是模型在训练集上预测的结果如何。这里我们需要实现 predict 函数。
如果一切正常的话,我们得到的在训练集上的准确率是0.89。
1 | # 预测函数 |
正则化逻辑回归
在这部分的练习中,你将实现正则化的逻辑回归算法,并用它去预测制造工厂生产的芯片能否通过质量保证(QA)。在 QA 中,一块芯片需要通过多个测试以确保它能够正常工作。
假设你是工厂的产品经理,并且你有了一些芯片在两种不同测试中的结果。你将根据测试的结果来判断是否应该接受这批产品。为了帮助你做出决定,你可以使用过去的芯片的测试结果来建立一个逻辑回归模型。
可视化数据
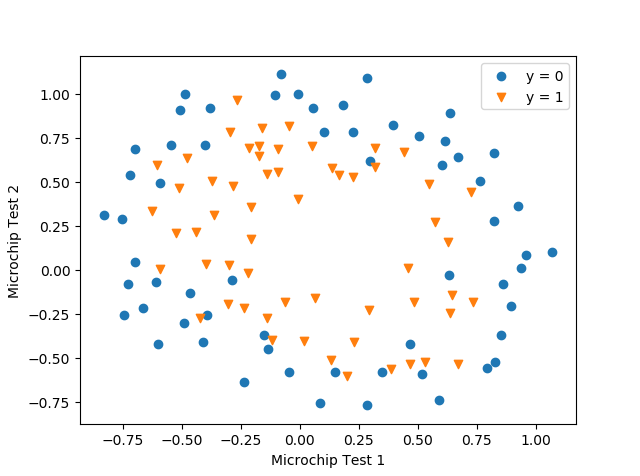
与前面的练习相似,使用 plotdata 函数是数据可视化,如下图所示,坐标轴是两次测试的分数,正例(y = 1 , 接受),反例(y = 0,拒绝)样本使用不同的符号显示。
从上图中我们可以知道,我们的数据集中的正例和反例不能使用直线来分割。直接将逻辑回归应用在这个数据集中效果可能并不好,因为常规的逻辑回归只能得到线性的决策边界。
特征映射
通过每个数据点来创造更多的特征可以更好的适应数据。在函数 mapFeature 中,我们将 x1 和 x2 映射到所有的 6 次多项式。
$$
mapFeature(x) = \begin{bmatrix}
x_1 \\ x_2 \\ x_1^2 \\ x_1x_2 \\ x_2^2 \\ x_1^3 \\ …\\ x_1x_2^5 \\ x_2^6
\end{bmatrix}
$$
我们将两个特征(在两个 QA 测试中的分数)转换成了 28 维的向量。一个逻辑回归的分类器在这样的高维向量上训练会得到更复杂的决策边界,当在 2 维的图像上绘制时,会呈现出非线性。
尽管特征映射可以使我们构建出更有表现力的分类器,但同时它也更容易过拟合。
在下一部分的联系中你将实现正则化的逻辑回归,同时你也可以看到正则化是如何作用在过拟合问题上的。
1 | def mapFeature(X1,X2): |
代价函数和梯度
现在你将编码实现计算正则化逻辑回归的代价函数和梯度。
回忆一下逻辑回归中正则化的代价函数。
$$
\large
J(\theta) =
\Huge[ \large -\frac{1}{m}\sum_{i=1}^m y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)})) \Huge]\large
+ \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2
$$
注意你无需正则化参数 $\theta_0$。
代价函数的梯度是一个向量,定义如下:
$$
\large
\frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
\qquad \qquad for \qquad j = 0 \\\
\frac{\partial J(\theta)}{\partial \theta_j} = (\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)})
+\frac{\lambda}{m}\theta_j
\qquad \qquad for \qquad j\not ={0}
$$
当你完成函数 costFunctionReg 时,使用初始化为 0 的参数 $\theta$ 得到的结果应该是0.693。
1 | def costFunctionReg(theta, X, y, my_lambda): |
学习参数
与前面的部分相似,这里我们使用 python scipy 库中的 optimize 函数来优化。
1 | result = op.minimize(fun=costFunctionReg, x0=initial_theta, args=(X, y,my_lambda), method='TNC', jac=gradient) |
绘制决策边界
参数 lambda 的不同,会影响最后模型的结果,我们来观察一下。
lambda = 0的时候,从下图中可以看到,这时相当于不进行正则化,已经出现了过拟合的情况, Train Accuracy: 87.28813559322035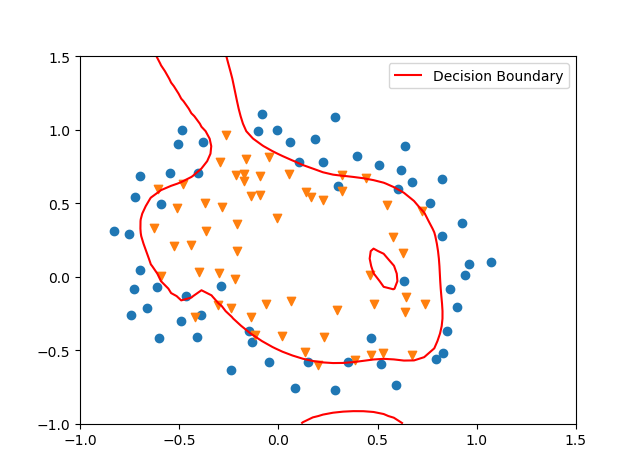
lambda = 1,此时的效果是最好的, Train Accuracy: 83.05084745762711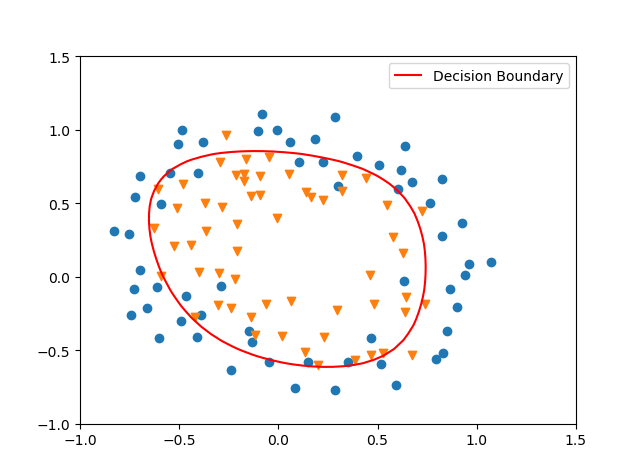
lambda = 10,此时的 Train Accuracy: 74.57627118644068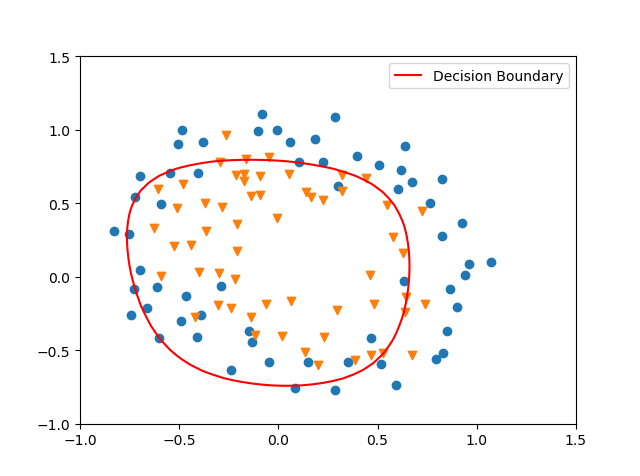
lambda = 100,此时的 Train Accuracy: 60.16949152542372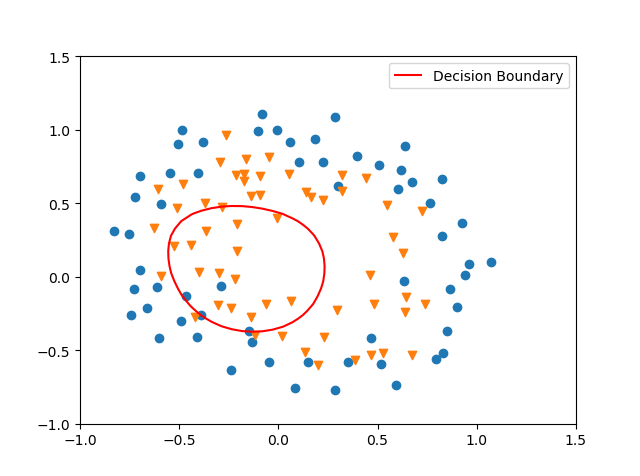
1 | # 绘制决策边界 |


