过拟合
定义:如果我们有太多的特征,这时训练出的假设能很好地拟合训练集(代价函数的值约等于0),当不能很好地泛化到新的样本中。泛化是指一个假设模型应用到新样本的能力。
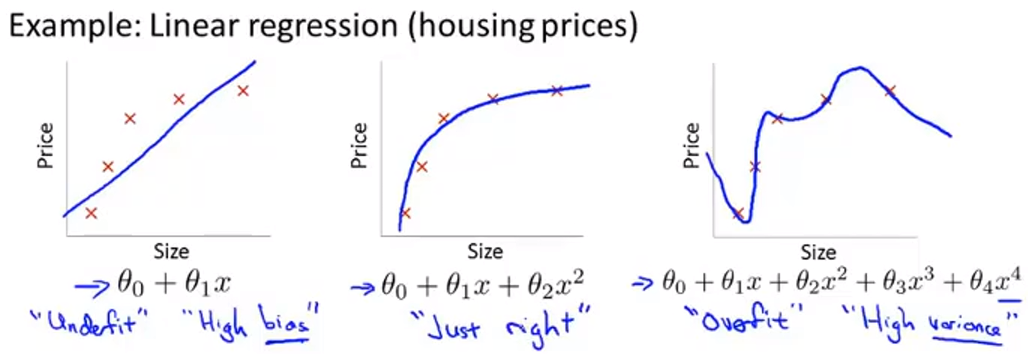
解决过拟合
- 减少特征的数量
- 人工选择需要保留的特征
- 模型选择算法
- 正则化
- 保留所有特征,减小参数$\theta$的值
- 当我们有很多特征,且或多或少都对预测 y 有影响,正则化也可以工作的很好
正则化
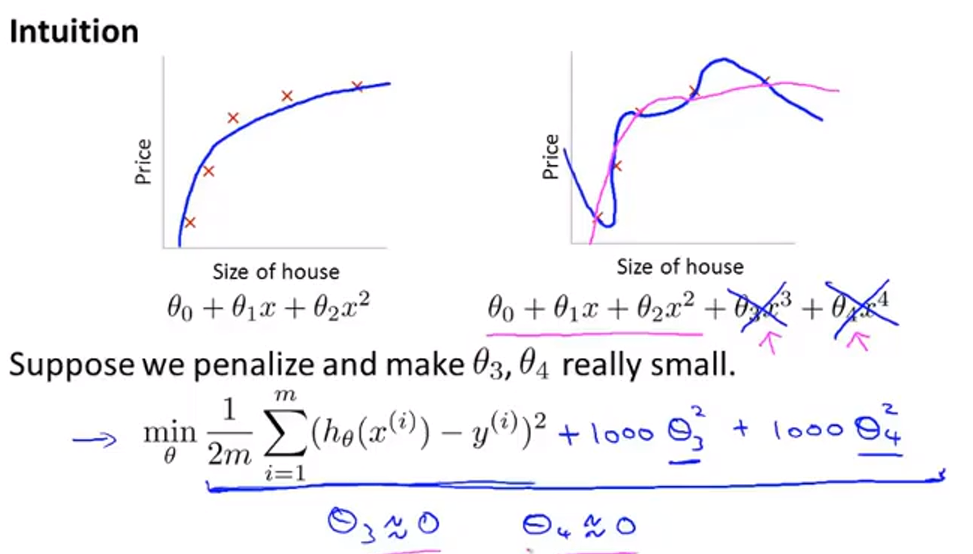
我们给代价函数新增了两项,并给 $\theta_3$ 和 $\theta_4$加上很大的系数,这样为了让代价函数的值最小,$\theta_3$ 和 $\theta_4$的值就会趋近与 0。最后的效果就好像我们在假设函数中直接去掉了这两项一样。
$$\Large Features:x_1,x_2,…,x_{100} $$
$$\Large Parameters:\theta_0,\theta_1,\theta_2,…,\theta_{100}$$
事实上,我们的问题中可能会有很多特征,但事先我们不知道该选择哪一个来缩小它们的值,所以我们需要缩小所有的值。
如此,代价函数需要作出这样的修改:
$$
\Large J(\Theta)=\frac{1}{2m}
\Huge[
\Large\sum_{i=1}^{m}{({h_\Theta}({x}^{(i)})-{y}^{(i)})}^{2}+
\lambda\sum_{i=2}^m\theta_j^2
\Huge]
$$
其中 $\lambda\sum_{i=2}^m\theta_j^2$ 是正则项,$\lambda$ 是正则化参数。
当我们的正则化参数 $\lambda$ 设置的过大时,可能会造成欠拟合的情况。因为此时的参数 $\theta_j$ 都已经趋近于 0。
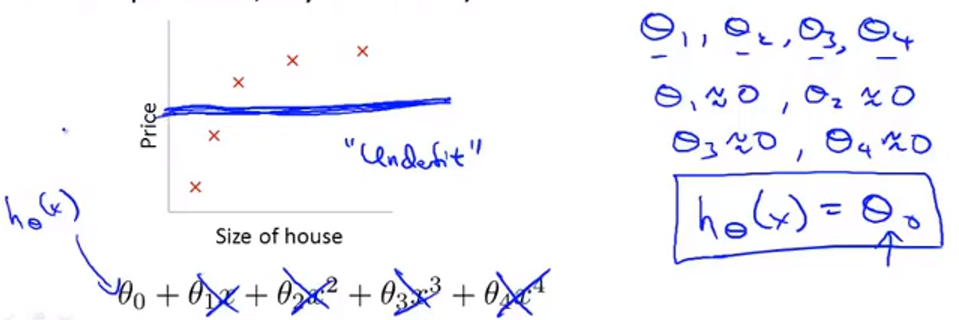
线性回归的正则化
梯度下降
$$ \Large repeat\left\{ \begin{aligned} \Theta_0 = \Theta_0-\alpha\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))x_0^{(i)} \qquad \qquad\\ \Theta_j = \Theta_j-\alpha\sum_{i=1}^m(h_\theta(x^{(i)}-y^{(i)}))x_j^{(i)} +\frac{\lambda}{m}\theta_j , j\not ={0} \end{aligned} \right\} $$这里我们的 $\theta_0$ 并不需要正则化。
正规方程
$$\large X = \underbrace{\begin{bmatrix} (x^{(1)})^T\\ (x^{(2)})^T\\ (x^{(3)})^T\\ ....\\ (x^{(m)})^T\\ \end{bmatrix}}_{m * (n+1)} \qquad y = \begin{bmatrix} y^{(0)} \\ y^{(1)} \\ y^{(2)} \\ ... \\ y^{(3)} \end{bmatrix} \qquad $$这时原来的方程
$$\large\Theta = (X^TX)^{-1}X^Ty$$
我们为其添加新的一项
$$\large \Theta = (X^TX \qquad
\underbrace{\lambda\begin{bmatrix}
0 & … & 0 \
… & 1 & … \
0 & … & 1 \
\end{bmatrix}}_{(n+1)*(n+1)})^{-1}X^Ty$$
这样就实现了正规方程的正则化。
By the way,当 $\lambda$ 大于0时,括号内的矩阵肯定是可逆的。
逻辑回归的正则化
代价函数
在逻辑回归中代价函数也做了相应的变化
$$
\large
J(\theta) =
\Huge[ \large -\frac{1}{m}\sum_{i=1}^m y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)})) \Huge]\large
+ \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2
$$


